고정 헤더 영역
상세 컨텐츠
본문
KNN(K-최근접이웃) 이란?
패턴 인식에서, k-최근접 이웃 알고리즘은 분류나 회귀에 사용되는 비모수 방식이다. 두 경우 모두 입력이 특징 공간 내 k개의 가장 가까운 훈련 데이터로 구성되어 있다. 출력은 k-NN이 분류로 사용되었는지 또는 회귀로 사용되었는지에 따라 다르다.
베이지안 분류기는 데이터의 확률분포함수를 미리 가정하고 이를 추정하여 분류에 활용하는 모수적 접근 방법을 취한다. 그러나 미리 가정된 확률 모델이 주어진 데이터 분포에 적합하지 않은 경우에는 좋은 성능을 기대하기 힘들다. 이러한 문제에 대한 대안으로 비모수적 밀도추정에 기반을 둔 K-근접이웃 분류기를 사용할 수 있다.(박혜영, 패턴인식과 기계학습)
K-근접이웃 분류기는 주어진 데이터로부터 거리가 가까운 순서대로 K개의 데이터를 찾은 후, 그중 가장 많은 수의 데이터가 속한 클래스로 할당하는 방법입니다. 이 분류기는 정규 베이즈 분류기에 비해 매우 비선형적인 결정경계를 가지며, 비모수적인 방법에 기반을 두므로 데이터의 분포 형태에 따라 성능이 크게 좌우되지는 않습니다.
K-근접이웃 분류기의 경우 새로운 데이터가 주어질 때마다 학습데이터 집합 전체와의 거리 계산을 통해 K개의 이웃 데이터를 선정해 주어야 하기때문에 계산 시간이 오래 걸리며, 항상 학습데이터를 저장하고 있어야 하는 문제가 있다. K-근접이웃 분류기를 실제 적용할 때는 K 값을 어떻게 정해야 할지도 문제가 되는데, 만일 K=1인 경우는 가장 가까운 하나의 데이터에만 의존하여 클래스를 결정하기 때문에 노이즈에 민감한 결과를 얻게 된다.
반대로 K 값이 너무 커지면 주어진 데이터 주변의 영역만을 중심으로 분류가 수행되는 것이 아니라 전체 데이터 영역에서 각 클래스가 차지하는 비율에 따라 분류가 수행되기 때문에 선형결정경계와 형태가 유사한 결과를 얻는다. 보통 전체 데이터의 수가 N일 때 K=sqrt(N)을 사용할 수 있지만 검증데이터를 활용하여 분류를 수행해 봄으로써 가장 좋은 성능을 주는 값을 찾는 방법도 생각해 볼 수 있다. (박혜영, 패턴인식과 기계학습)
여기서는 OpenCV에서 제공하는 K-근접이웃 분류기를 사용하여 간단한 2차원 데이터를 분류하는 예제 코드를 작성해 보았습니다. 아래 첨부 코드를 참고하시기 바랍니다.
import numpy as np
import cv2
def on_k_changed(pos):
global k_value
k_value = pos
if k_value < 1:
k_value = 1
trainAndDisplay()
def addPoint(x, y, c):
train.append([x, y])
label.append([c])
def trainAndDisplay():
trainData = np.array(train, dtype=np.float32)
labelData = np.array(label, dtype=np.int32)
knn.train(trainData, cv2.ml.ROW_SAMPLE, labelData)
h, w = img.shape[:2]
for y in range(h):
for x in range(w):
sample = np.array([[x, y]]).astype(np.float32)
ret, _, _, _ = knn.findNearest(sample, k_value)
ret = int(ret)
if ret == 0:
img[y, x] = (128, 128, 255)
elif ret == 1:
img[y, x] = (128, 255, 128)
elif ret == 2:
img[y, x] = (255, 128, 128)
for i in range(len(train)):
x, y = train[i]
l = label[i][0]
if l == 0:
cv2.circle(img, (x, y), 5, (0, 0, 128), -1, cv2.LINE_AA)
elif l == 1:
cv2.circle(img, (x, y), 5, (0, 128, 0), -1, cv2.LINE_AA)
elif l == 2:
cv2.circle(img, (x, y), 5, (128, 0, 0), -1, cv2.LINE_AA)
cv2.imshow('knn', img)
# 학습 데이터 & 레이블
train = []
label = []
k_value = 1
img = np.full((500, 500, 3), 255, np.uint8)
knn = cv2.ml.KNearest_create()
# 랜덤 데이터 생성
NUM = 30
rn = np.zeros((NUM, 2), np.int32)
# (150, 150) 근방의 점은 0번 클래스로 설정
cv2.randn(rn, 0, 50)
for i in range(NUM):
addPoint(rn[i, 0] + 150, rn[i, 1] + 150, 0)
# (350, 150) 근방의 점은 1번 클래스로 설정
cv2.randn(rn, 0, 50)
for i in range(NUM):
addPoint(rn[i, 0] + 350, rn[i, 1] + 150, 1)
# (250, 400) 근방의 점은 2번 클래스로 설정
cv2.randn(rn, 0, 70)
for i in range(NUM):
addPoint(rn[i, 0] + 250, rn[i, 1] + 400, 2)
# 영상 출력 창 생성 & 트랙바 생성
cv2.namedWindow('knn')
cv2.createTrackbar('k_value', 'knn', 1, 5, on_k_changed)
# KNN 결과 출력
trainAndDisplay()
cv2.waitKey()
cv2.destroyAllWindows()
k 가 1 일때 녹색점과 파랑색점에 판별을 아래와 같이 된다. 눈으로 볼때는 파랑점의 경우 더 가가운 위치는 초록색이다. 이는 노이즈로 판별할 수 도 있다. 다음은 k 값을 3으로 올려보도록 하겠다.

K 가 3일때 초록색점의 판정이 애매한 위치로 판정된다. 가장 가가운 위치는 빨간점에 더많은 가중치가 있는 것으로 눈으로 판정된다. 다음은 K 의 값을 5로 하고 결과를 확인 해 보겠다.
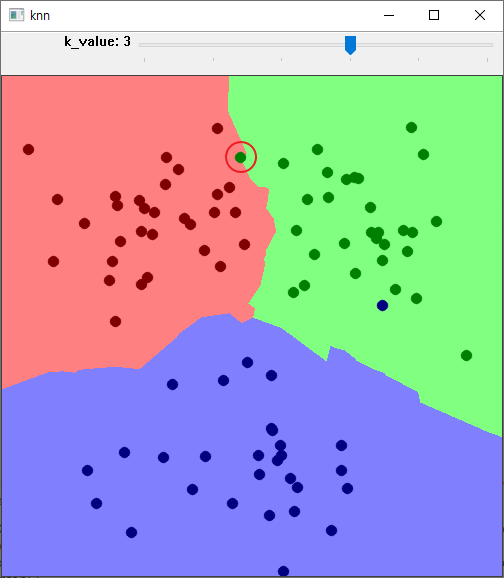
K 의 값이 5일때 초록색점은 빨간영역에 포함된다.

K 의 값에 따라 추정치에 변화가 있을 수 있다. overfitting 또는 underfitting 이 나타날수 있다. 분류를 알 수 없는 데이터에 대해 가장 가까운 이웃 k개의 분류를 확인하여 다수결로 분류할 수 있다. K 추정치의 값은 아래 블로그를 참고 하기 바란다.
hleecaster.com/ml-knn-concept/
K-최근접 이웃(K-Nearest Neighbor) 쉽게 이해하기 - 아무튼 워라밸
본 포스팅에서는 머신러닝에서 사용할 K-최근접 이웃(K-Nearest Neighbor)에 대한 개념 설명을 최대한 쉽게 설명한다. 정규화(normalization), k개수에 따른 과적합(overfitting), 과소적합(underfitting)에 대한
hleecaster.com
'영상처리 > OpenCV 실습' 카테고리의 다른 글
| 사진에서 손상된 영역을 복원 - 인 페이팅 By OpenCV (0) | 2021.06.15 |
|---|---|
| OpenCV 문서 스캐너 구현하기 (2) | 2021.05.25 |
| 이미지 슬라이드 쇼 실습 (0) | 2021.05.12 |
| KNN 으로 필기체 인식하기 (0) | 2021.03.29 |





댓글 영역